丘成桐中心李铁香教授团队于SIAM Journal on Scientific Computing (Vol. 46, No. 6, 2024) 上发表了题为“An SVD-Based Fast Algorithm for 3D Maxwell’s Equation with Perfect Electric Conductor and Quasi-Periodic Boundary Conditions” 的学术论文。中心吕星龙博士为本文的第一作者,李铁香教授为通讯作者。

这篇论文介绍了一种快速算法以用于计算具有超胞结构和完美电导体以及准周期混合边界条件的三维光子晶体的能带结构。斜 Yee 有限差分方法被用于统一离散化无源频域麦克斯韦方程,可以平等地处理各种布拉维晶格。通过巧妙地分析出离散微分算子的两两共享左右奇异向量的重要性质,文章中进一步给出了混合边界条件下离散旋度算子的显式奇异值分解。基于零空间压缩技术和FFT等技术,实现了三维光子晶体能带结构的高效求解。
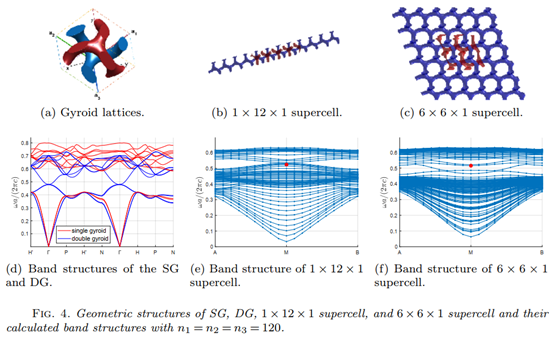
丰富的三维光子晶体能带结构数值实验充分展示了算法在GPU平台上的高效能和计算稳定性。更重要的是,这篇文章成功模拟了单陀螺和双陀螺结构的耦合模型,展现了其特殊的边缘态现象,朝拓扑光子晶体的高效仿真迈出了一大步。
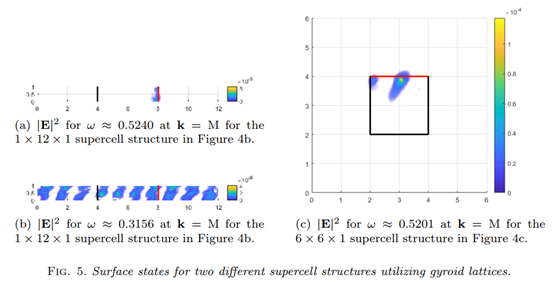
这项工作是对李教授团队此前相关工作“FAME” (http://www.njcam.org.cn/fame/index.phtml) 的重要深化和延伸,有望推动新型材料高效仿真算法在相关领域的自主开发应用,对光子晶体的优化设计和新型光学器件的研发具有重要推进作用。李教授团队在北太天元4.0 (https://www.baltamatica.com) 中发布的仿真插件FAME V2.0有利用到该论文的相关技术。
(供稿:吕星龙)
