引力与场论的全息对偶是目前人们研究引力的量子性质以及时空的量子信息起源等重要问题的主要渠道。该研究方向的一个重要切入口是,找到刻画边界场论中量子纠缠结构的信息量与对偶引力理论中几何量的对偶关系。其中最著名的成果是2006年由Ryu和Takayangi提出来的RT准则,这条准则将边界共形场论的纠缠熵与AdS时空中的最小曲面联系起来,从而开创了在全息对偶框架下,通过研究量子场论的纠缠结构来理解引力时空起源的重要研究方向。除了植根于边界的极小曲面之外,最近几年关于纠缠楔最小横截面(EWCS)的全息对偶研究吸引了相当大的关注,学界提出了多种可能与之对偶的量子信息量,比如纠缠纯化(entanglement of purification)、反射熵(reflected entropy)以及纠缠负模(entanglement negativity)等等,但多数信息量的计算都极其复杂,并且与EWCS的对偶关系没有得到严格的证明。
2021年以来,东南大学丘成桐中心的文强副教授提出满足某种平衡条件的部分纠缠熵——平衡部分纠缠熵(BPE)很有可能是对偶于EWCS的量子信息量[1],并且在多种全息理论中验证了这个猜测。相比于其他量子信息量,BPE有很多优点,比如计算简单、可以定义在混合态的一般纯化下、可以定义在超出AdS/CFT的全息理论中、可以在非全息的场论或凝聚态体系中定义。并且在正则纯化下BPE的定义与反射熵等价。在[2]中,文强与合作者验证了BPE的纯化无关性从而支持BPE是一种內秉的可以刻画混合态量子纠缠的信息量,并且证明了BPE有基于优化问题的定义。在[3]中,文强与博士生钟浩成一起,将EWCS的概念推广到了带有引力反常的全息理论中,并且验证了BPE与EWCS的对偶关系。
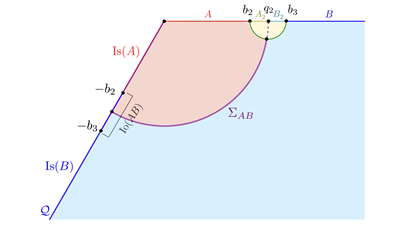
近日,文强与印度理工博士生Debarshi Basu、中国科学技术大学博士后林炯以及南方科大博士后卢一洲,在知名物理学综合期刊《Scipost Physics》上再次发文[4],研究了有纠缠岛情形下BPE的定义和计算,并且验证了BPE与EWCS的对偶关系。文章中提出的新概念——无主纠缠岛(ownerless island)扮演了关键性的角色(下图中Io(A,B)区域)。文强团队发现基于无主纠缠岛对纠缠熵贡献分配的不同方案,所得到的BPE对应于纠缠楔中横截面不同的saddle point,进一步非平凡地验证了BPE与EWCS的全息对偶关系。
纠缠岛相的提出为人们理解黑洞信息丢失疑难提供了全新的思路。纠缠岛不仅仅可能是量子引力的一种內秉性质,更重要的是纠缠岛相也很可能定义在非引力的量子体系。文强与合作者发表的这篇文章[4],对于人们理解纠缠岛相下系统的纠缠结构有重要的启发性。
[1] Q. Wen, Balanced partial entanglement and the entanglement wedge cross section, J. High Energy Phys. 04, 301 (2021).
[2] H. A. Camargo, P. Nandy, Q. Wen and H. Zhong, Balanced partial entanglement and mixed state correlations, SciPost Phys. 12, 137 (2022).
[3] Q. Wen and H. Zhong, Covariant entanglement wedge cross-section, balanced partial entanglement and gravitational anomalies, SciPost Phys. 13, 056 (2022).
[4] D. Basu, J. Lin, Y. Lu and Q. Wen, Ownerless island and partial entanglement entropy in island phases (2023), SciPost Phys. 15, 227 (2023).
