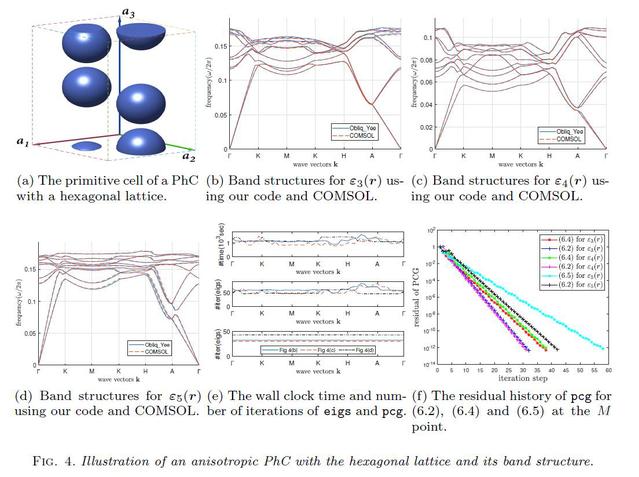
光子晶体是一种实现高效光子集成器件的新型光子人工带隙材料，在科学界和产业界被称为“光半导体”或“未来的半导体”，被誉为二十一世纪最具潜力的新型材料。光子晶体能带结构的快速仿真在光学和材料科学领域具有重要意义，该论文研究了三维各向异性光子晶体能带结构的快速算法，通过直接使用以晶格平移向量为基底的斜坐标系和 Maxwell 方程的协变表述，提出了一种可以统一处理正交及非正交布拉维晶格、各向同性及各向异性介质的算法框架，特别的是，该算法框架在离散化过程中可以轻松处理电磁场的布洛赫条件。在将频域 Maxwell 方程组离散化为标准代数特征值问题后，利用矩阵分析的技巧对其进行模型压缩，便可将该问题直接被转化无零空间的标准特征值问题，结合求逆Lanczos算法可轻松得到其最小的几个正特征值和相应的特征向量。论文中，该算法与商业软件 COMSOL中进行了大量数值比较，充分展现了新算法的有效性和高效性。

  


       该项研究工作无论是对基于矩阵计算的大规模科学计算的数学理论方法研究，还是对新型材料的最优结构设计和性能研究提供数值依据，都充分显示了南京应用数学中心在交叉学科方面的优势。基于此，南京中心B项目组对三维光子晶体能带结构实现了高效数值仿真，设计了基于GPU高性能计算技术的软件包 “FAME”，相关程序和数据发布在本中心的网站http://www.njcam.org.cn/fame/index.phtml 上，有望推动新型材料高效仿真算法在相关领域的自主开发应用。



（原文转载自：南京应用数学中心网站，

http://www.njcam.org.cn/results/20230807/i764.phtml）