东南大学120周年校庆大师讲座专场
作者:丘成桐,东南大学丘成桐中心主任,南京应用数学中心主任,北京雁栖湖应用数学研究院院长,清华大学数学科学中心主任,美国科学院院士,中国科学院外籍院士;菲尔兹奖、克拉福德奖、沃尔夫奖、马塞尔·格罗斯曼奖得主。
(以下文本为丘成桐院士于2022年6月1日在“东南大学120周年校庆大师讲座”系列的演讲讲稿,原文刊登于《数理人文》(微信订阅号:math_hmat)。未经许可,不得转载。)
(本演讲可通过以下链接观看录播:丘成桐:数学之美与应用 (koushare.com))
今天,我很高兴接受邀请,庆祝东南大学成立一百二十年的校庆。
我和东南大学比较密切的来往应该是从十多年前开始。我在东南大学九龙湖校区作了一个演讲,那天是圣诞节,大雪纷飞。在美国圣诞节是假期,没有想到报告厅中却坐满了同学,同学们反应热烈,还引用了我作的一幅对联,使我惊喜。当时东南大学的学生说,他们对以下的对联:
行乎名利之途,入乎公卿之门,虽荣受赏,吾不谋也。
得乎造物之贞,乐乎自然之趣,虽穷有道,文其兴乎。
在古书中找不到出处,问我在什么地方可以找到。我看到这是我从前讲辞的一部分,有点惊喜,没想到东大年轻的学生看文章会这样小心,做学问有严谨的态度确是好事!
当时我只知道东南大学历史悠久,一百年前是中国南方最重要的大学,以后国民党政府将它改名为中央大学,一代宗师吴健雄先生就读于此。但是以后才知道,我的老师陈省身先生在清华大学的硕士生导师孙光远先生离开清华大学以后,长驻此处。

吴健雄(左)、孙光远(右)
以后,张广军校长三顾我于清华大学,坚持请我帮忙东南大学成立数学中心,意诚辞恳,使我觉得不担负起这个责任,太不讲究人情了,也对不起国家要建立基础科学的重任。今年张校长另有重任,应该还记得我们一起建立中国基础科学的共同志愿!

最近,求真书院邀请清华大学美术学院刘巨德教授作讲座,题为《混沌的故事》,讲述艺术家眼中的美。每一个学者对美都有不同的见解。我为大家讲一讲数学家和科学家眼中的美。

刘巨德教授
我认为世界上的美必须以真理为基础,才称得上“美”。刘教授说,美是划时代、超越时空的。然而,超越时空、唯一能够存在的只有真理。我坦白讲,真理其实只有一个——那就是数学。没有一个学科能像数学一样,对世界的描述经得起时间考验。从古希腊学者、牛顿、爱因斯坦,到今天,人类对世界的观察以及据此形成的理论,不停地在变化;在实验室中,由于技术精益求精,观察到物质世界中不一样的结果,推翻了以往的 结论。
物理的理论没有实验的证明都是空洞的,但是实验本身并不是无懈可击。记得一位物理学家说过,假如我们出海去捕鱼,用的网都有十寸大的空隙,捕捉到的都会是庞大的鱼,结论可能是:海洋中的鱼都是庞大的。随着渔网不断的改进,捕捉到鱼的种类愈多,结论就不停地改善。但是渔网的密度终是有限的,到一个精度以后,需要改变方法。
在某个地方、某个时间用有限的样本,得到的结果是否在其它地方、其它时间适用,是一个大问题。牛顿引力定律在地球上可以应用,到了外太空,居然还是可以用得着,这个是十分值得惊讶的事情!牛顿用微积分推导出开普勒的天体运行公式,使人震撼!物理学的基本定律有这种万有的适用性,是物理学和数学能够相辅相成的原因!我认为,任何能够普遍性地描述自然规律的科学,必须是由数学来表达,因为天下间唯一不变的科学理论只有数学。
何以故?因为研究一切科学,必先有其概念的假定!这种假定自非绝对的知识,要批判这种假定之是否正确,往往系于科学家对宇宙了解的深入与否。十九世纪以前的物理学家以为空间和时间是分开的,空间是连续的。对于当时的科学家,日常生活见到物质的速度远远比不上光速,量子的观念也还未正式开始。牛顿力学的假定基本上成立,大家都很满意。
相对论和量子力学使得二十世纪的科学家产生了不同的观点,改变了古典的物理学,使我们对于我们的宇宙有更深一层的了解。无论是极小质子的结构,或者是遥远的太空。我们见到的现象都是前人难以想象的。我们在巨型对撞机中产生了很多不同的基本粒子,在太空中看到遥远的星云,也从大型的观察中,找到黑洞存在的有力证据。到了廿一世纪,暗物质、引力波、量子引力理论成为主流。因此在某种意义下,我们眼中看到的物理学的真理是不停地在改变。
在这一串宏伟的科学发展中,数学家做出了巨大的贡献。在很多重要的基础物理学的发展场合中,数学家靠前,带领着物理学家向前走,然后群策群力地去了解我们的宇宙。
举个重要的例子,我们来回顾科学界中一个极为重要的发展:牛顿的伟大贡献之一,是引发了微积分在物理学上的重要应用,从而引起了数学本身的革命。到了十九世纪初,高斯和黎曼为了对电磁深入了解,他们发展了一套数学理论,这套理论最后由麦克斯韦完成,建立了完美的麦克斯韦方程组。

从左至右:牛顿、高斯、黎曼、麦克斯韦
在廿世纪初,外尔通过另外一个观点来解释这个方程组,使它们成为他提出的规范场的一部分,他也是第一个提出规范原理的数学家,这些观念成为现代科学的基础。但是我们也应该知道,在 1926 年时,法国几何学家嘉当发展了联络理论,也就是我们今天说的非交换规范场论。
外尔(左)、嘉当(右)
以后大量的数学家,包括陈省身先生在内,参与非交换规范场的研究,古典的规范场可以说是全部由几何学家完成的。但是规范场的在物理学上的量化工作要等到上世纪六十年代才由几个大物理学家完成。到了七零年代,理论物理的标准模型成为基本科学中最重要的工作。在上述的工作中,用到极为深奥的数学理论。这些理论,已非当年的物理学家所能吸收。
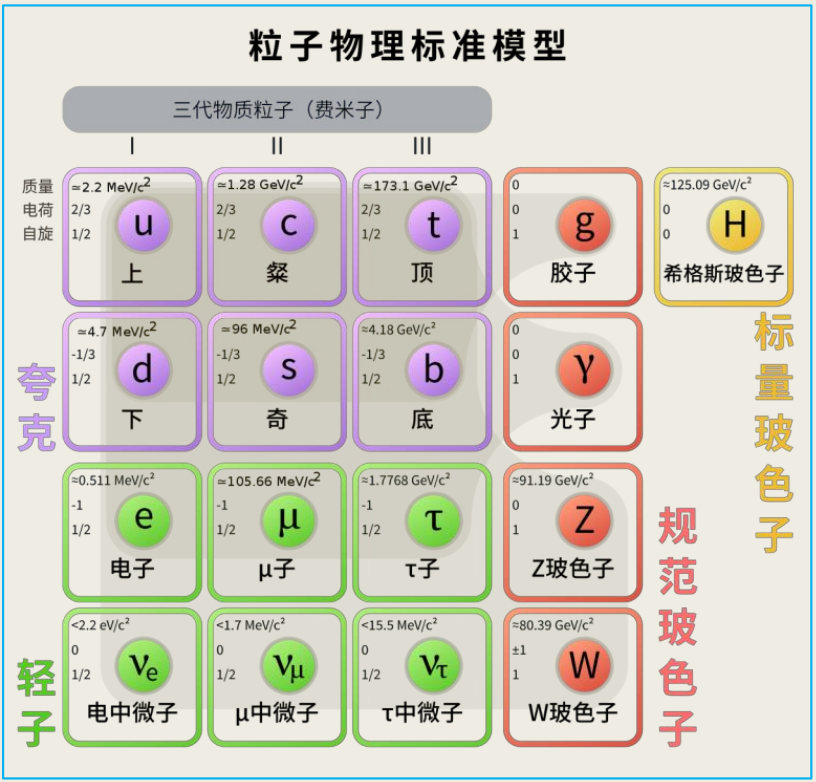
物理学家对真理的了解不停在改变,但是其中的数学理论从来没有人质疑过它们的正确性。因为它们的基础是一些难以质疑的假设,这些假设是最简单的逻辑系统,这些系统也是人类一切文明的基础。可以说,
天地万物可以改变,惟独数学真理不能改变!
数学家用严格的逻辑系统建设了不同的数学系统来描述大自然,从中看到统领大自然的规律,在这个过程中我们看到大自然如何建立自己的结构,它瑰丽壮观,万物难以比拟!
大道至简,是对数学之美的归纳。最简单的数学,从1=1开始,到1+1=2,1+2=3,不停推导下去。人类通过这种方式,认识到自然数,从而有了数学。人类从数学诞生之初,计算牲畜、税收时,就认识到这一点,历经千年,从未改变。这个抽象概念,是对事物精妙地归纳和总结。这与美有着密切的关系。数学把现实抽象为真理,美建立于真理之上,同时,美引导着人类不断发现真理。没有对美的追求,人类很难察觉真理的存在。数学的发展,就是有赖于人类对美的追求,感知真理,并找到真理之所在。
时代交替,物理学家在现象界观察得到的理念也在不断更迭。只有数学是唯一亘古不变的、超越时间和空间的真理。唯一改变的,是我们对其认识的深度和广度。2000多年前,古希腊学者开始了对数学之美的追寻。
随着人类的感受能力、学习能力不断变化,数学这门学科也发生了不少变化。这是个很有意思的过程。可以说,数学是一个重要的桥梁,是美与真理之间的桥梁。没有这个桥梁,我们无法真正理解所谓“真理”,也无法从对美的感官体会,上升至对真理的理性认知。洋务运动倡导“西学为用、中学为体”,但并没有搞清楚西方科学文化的核心是把数学视作一个主要的桥梁,我们必须了解它、认识它。
举一个直观的例子。画家喜欢画竹子,它优雅、坚韧、颇有风骨,折射了中国知识分子许多精神层面的追求。对于数学家来讲,第一眼看到竹子,是什么呢?那是一条直线,这是第一印象。画家描摹竹子的风骨,有很多手段。数学家也会为这条直线增加许多内容。
第一眼看竹子是一条直线。那么直线是怎么构造成功的呢?这对于数学家来讲, 是一个饶有趣味的事情。画家和物理学家不会在乎,但我们很在乎。为什么呢?首先,构造这条直线,我们引入了自然数,即整数,从 1、2、3、4 开始,这是一个基本的数学结构。在这条直线上,我们首先标注自然数;接着,为了继续丰富它的构造,我们接下来构造了分数,比如 1/2、3/4,密密麻麻地在这条直线上画起来。
下一步怎么办呢?希腊人构造了无理数。他们用一个垂直的线构造三角形,两边长为1,斜边的长度为√2 ——这就是希腊毕达哥拉斯学派的发现。√2是无理数,无法写成分数。构造无理数之后,我们在直线上又增加了一大堆数字,更密了一些。但这还不够,我们开始用圆规和直尺构造数字,但无论如何都没能填满这条直线。
差不多过了1500多年,我们才完全把直线填满,弄清楚实数的构造,把这条竹子变成一条完备的实线。大多数人觉得莫名奇妙,为了达到这个目标,数学家花了很多功夫,才终于对直线有了透彻的了解,现在是一清二楚了。这就好像画家费笔墨描摹竹子的意蕴,我们也用了不少抽象的数的概念构造直线。
画家笔下的波,其实跟虚数有密切关系。但是,目前还无法将富有活动力的波生动地画出来,这是因为我们对虚数的了解不够清楚。虚数是研究动力系统最重要的数字,量子力学也要用到虚数。从引入正整数如 1、2、3、4,发展到一条直线、到虚数、到完满地解释二维空间,这个过程其实是通过数学慢慢地、一步步地走完的。
从虚数到二维空间、到三维空间,一路来都是有条有理的推进。起到推动作用的,除了数学严格地推理之外,也有对美的追求。数学家希望达到什么目标呢?我们看到的现象,眼中的世界,应该尽量完备。如果存在一些空间,我们尚无法描述,不行,我们必须理解透彻,要从数学角度绘制一个完美的图像。在数学家眼中,这个图像犹如一幅图画。从整数的点加上去变成一条直线——这令人满意。但是还不够,加上虚数,就可以描述二维空间;二维空间还是不够,一路加上去。
应该有人会说,竹子明明不是一条线,为什么数学家这么笨,将它看作是一条线!这当然是个正确的问题。竹子的表面是一个圆柱,直线不过是描述竹子特征的第一步,这一步并不完全符合物理现象,但是我们用实数来描述直线却是绝对正确而严谨的。
对构造直线的实数越来越了解,但并不足够满足数学家的好奇心。在15世纪的时候,我们开始引入了虚数,这将我们关注的空间加大了:从一条直线变成二维空间——认知二维空间是人类历史上一个很重要的事情。虚数产生以后,我们对很多波动方程、波动的种种现象都了解清楚不少。
第二步,我们继续描述竹子。找一个固定半径的小圆圈,它和直线垂直,圆心沿着直线拉出去,就可以得到我们期待的圆柱。而描述这个圆柱最佳的数学方法是复数。加上复数的结构后,圆柱在数学上叫做黎曼面。黎曼面在描述二维空间及在现代物理学中的应用广泛,实在是威力无穷。
当上述小圆圈的半径变得很小时,圆柱就是一条直线,这是高维空间能够用来描述低维度的现实界的一种方法。圆圈的半径随着圆心的位置变动时,圆柱可以变成竹节。就是这样,我们一步一步地接近现象界的竹子!而且每一步都有严格的数学的描述。
几何学家看竹子,可以用上述的观点,但是西方科学革命的领导人伽利略大概不会这样看,他会研究竹子的种种物理性质,例如弹性、结构性等问题。这些问题到了牛顿力学和微积分出现后,得到了更完美的解决,数学家如费马、欧拉、拉格朗日一直参与其事。

从左至右:伽利略、费马、欧拉、拉格朗日
和伽里略差不多時候,中国明朝最出色的哲学家王阳明想了解朱熹“格物致知”的看法,花了三天三夜去格竹,结果没有得到任何结果。他决定“心即理”、“心外无理,心外无事,心外无物”、“夫万事万物之理,不外于吾心,而必曰穷天下之理,是殆以吾心之良知为未足,而必外求于天下之广。以俾补增益之。”(《传习录》)
其实数学的结构,从公理出发,不假外求,可以说纯出于心!然而数学内由心生,外则可以审物之真实意义,甚至社会人事之结构,数学皆可为其骨干!
反过来说,假如数学没有外物的表现和刺激,就会变成空白玄论,了无内容!所以数学是心与物之唯一桥梁,真善美融合的骨髓。有了强大的数学基础,我们实在不需要诸如“中学为体,西学为用” 的讨论!
近代物理学中,我们可以将直线用三维或者四维的平坦空间来代替,而圆圈可以用更复杂的几何体来代替。一个重要的几何体就是卡拉比-丘(Calabi-Yau)空间,从中可以描述种种不同的物理现象。
所以说,数学家看一杆翠竹与画家或者艺术家不同。我们有条有理地通过推理不断加深理解,之后再描述它。现在,我们推理到三维空间,还是觉得不够。在 19 世纪,开始了四元数的发现。不久后,更发现了八元数,因而进入高维空间。高维空间能够表现更多生活的种种现象。高维空间是一个重要 的问题,有几十、几千、几万个粒子滚动时,形成一个高维空间。现在人工智能要到几千万维空间,高维空间里的种种现象,都很美。这里头有很多真理,即数学的存在。
这就是数学家眼中的世界,以及我们对美的追求。面对眼前的万千世界,那么多无法把握的现象,我们依靠美的指引,寻找其中的数学真理。从一根竹子,引出一条直线,到二维空间,逐渐进入高维世界,连结起来,不断丰富,发展出这个重要的学科。其中饱含了数学的精神,从简到繁,再用一个简单的道理描述大自然最复杂的现象,最终无限靠近真理。
无论是古希腊还是文艺复兴时代,这个精神一以贯之。文艺复兴时期的绘画艺术就与数学密不可分,从而促发了几何的发展——这也说明了美与数学从来都是密不可分的。
从古希腊直到今天,伟大的理论科学家都认为真理必须以简洁美丽的形象出现,同时都相信这些真理。必须放诸四海皆准,好的科学原理不止应用在某个现象而已。在数学上,有一个很有意思的做法:在欧式几何中,我们写下五个公理,要求我们的几何现象必须要满足这些公理,从这些看似简单的公理中,我们很惊讶地发现,从它们开始,同估计逻辑的方法,可以推导出很多意想不到的结果。
我老师陈省身先生关于示性类的工作,就是一个很好的例子。在1945年他做这些工作时,没有用公理化的方法。但是到了1954年的时候,希策布鲁赫(Hirzebruch)将他的理论公理化,发扬光大,成为数学和物理学中极为重要的工具。
公理化的好处是从根本处找到支撑我们研究方向的真谛,多一个公理和少一个公理,得到的结果可以完全不同!
古希腊哲学家很着重和谐这个观念,英国作家狄更生(Dickinson)著有《希腊人的人生观》,书中说:调和呦!就在这一字的意义上 ,我们可以有办法解说希腊文明的主要观念!(A harmony! And in the word we have the key to the dominant idea of Greek Civilization)。希腊人是美与善、身与心、个人与国家、神与人,调和为一的。希腊精神是入世的客观的,是讲究人与自然的调和。
这个精神也表现在数学里面:公理帮我们数学家将各种不同的现象统一起来,用几个十分明显的公理互相交错地编织成一幅漂亮的数学图画。这是调和观念的量化过程!
几何学多姿多彩,不仅有令人着迷的漂亮理论,还在现代工程实践中发挥着巨大作用。现代科技需要大量薄膜学的知识,因此如何精准描绘二维曲面是工程学不可缺少的学问。
二维曲面的研究可以追溯到伟大的科学家欧拉,他与牛顿同一时代,他用微积分来解释几何学,创造了变分法来计算一些重要的几何图形。黎曼和他的老师高斯毫无疑问是现代几何学的两 位奠基人。高斯是现代几何学的先父,而真正的创始人是黎曼,在十九世纪中期提出了黎曼几何和共形几何理论,不仅在理论物理中起到关键的作用,还在计算机图形学、几何建模、医学图像得到广泛应用。
黎曼的一个划时代的贡献就是提出了前面提到的“黎曼面”的概念,并引入了单值化的观念:虽然曲面表示在三维空间中无限维的自由度出现,但它们的保角结构却是有限维的!二维曲面存在一种全纯函数赋予的结构,也即共形几何。黎曼映照定理是说,![]() 中任何非空单连通区域
中任何非空单连通区域![]() 都可以双全纯地变换成单位开圆盘。之后再经过许多人的努力,这个漂亮定理才被充分了解,最后导致庞加莱(1882)及克莱因(1883)的单值化定理。
都可以双全纯地变换成单位开圆盘。之后再经过许多人的努力,这个漂亮定理才被充分了解,最后导致庞加莱(1882)及克莱因(1883)的单值化定理。
黎曼曲面的引进及其单值化定理是十九世纪的一个辉煌成果:任何二维曲面都可以看成是黎曼曲面;所有带度量的封闭紧曲面 都可以共形(保角)映射到三种标准空间中的一种:球面、欧式平面或者双曲平面。
单值化定理有非常重要的理论意义和现实意义,它极大地简化了很多曲面几何问题的理论证明和算法设计。
在1997年时,哈佛大学念计算机的顾险峰的原来导师离开了哈佛大学,他跑来找我做研究图像处理的问题,我建议把古典的共形几何方法用到图像学上。我们用黎曼曲面的方法发展出来的理论,以后发展成为图像学中重要的分支—计算共形几何。2002年之后,殷晓田(现在亚利桑那大学做教授)做我的博士后,将这些方法继续推进,也引进调和映照体积度量(harmonic map volumetric)及单网格的方法。
计算共形几何数学方面的核心脉络是证明单值化定理解的存在性、唯一性、正则性、适定性,特别是如何推广到离散曲面;计算机科学方面的核心是如何设计算法,计算出单值化定理。在计算机中,将光滑曲面用离散曲面来表示,将现代拓扑和微分几何中的理论推广到离散情形,用计算机去实现抽象的几何理念,可以得到很好的工程实践。
共形几何是研究共形变换下不变量的学问。所谓共形映射就是保持角度不变的映射。例如,我们将三维人脸曲面映射到二维平面圆盘,在人脸上随意画上两条相交的曲线,曲面上的曲线被映射到平面曲线,但是相交角度不变。由于保角变换具唯一性,因此很容易去做人脸比对。

共形变换将曲面的无穷小圆映到无穷小圆;一般的微分同胚将无穷小椭圆映到无穷小圆;如果无穷小椭圆的偏心率有界,那么微分同胚称为拟共形映射。
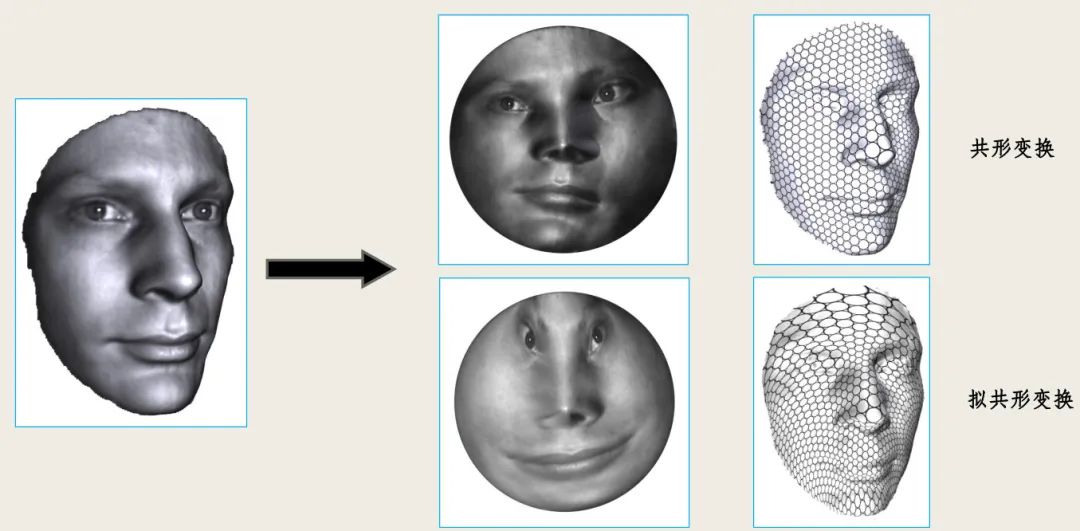
在 2005 年,我指导我的博士后雷乐铭用拟共形方法研究医学图像。几年后,我和顾险峰等人发现我刚刚博士毕业时和郑绍远在实蒙日-安培方程(real Monge-Ampere equation)和闵可夫斯基问题(Minkowski problem)上的一些方法可以推广并应用到最优传输的问题上去。
例如给定两张三维人脸曲面,上面标注着相应的特征点,我们希望找到微分同胚满足一一对应,同时此微分同胚尽量光滑,减小几何畸变。在通常情况下,满足这些限制的共形变换是不存在的。此时我们需要将共形映射拓广到拟共形映射。
在计算机图形学领域,计算共形几何应用于曲面参数化。曲面参数化是指用一个拓扑同胚将曲面映射到平面或者球面区域,使得映射的畸变尽量小。
通常畸变分成两类:角度畸变和面积畸变。
角度没有畸变的映射,被称为是共形变换;
面积元没有畸变的映射,被称为是保面积变换。
优化狄利克雷能量可产生共形变换,完全去除角度畸变;优化拉伸能量可以产生保面积变换(不唯一),完全去除面积畸变。实际应用中,保角参数化和保面积参数化各有优点。

在几何计算方向占据统治地位的是数值计算方法,部分归因于大多数几何问题不存在解析解,只能用数值解加以近似。高效的数值计算方法与现代几何的理论的有效结合,可将抽象的几何理论转换成计算机算法,用于处理工程和医疗实践中的三维几何数据。
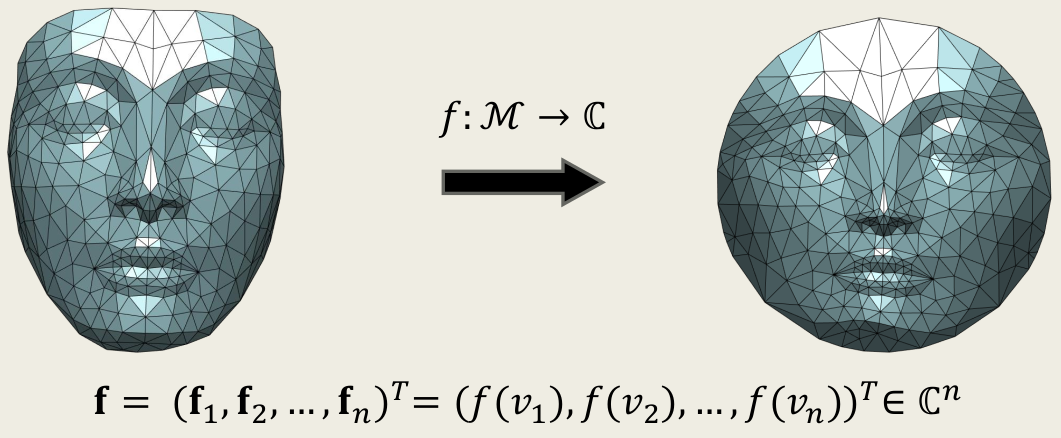
例如,与三维扫描技术结合,我们利用共形变换实现三维人脸动态图片的曲面参数化。
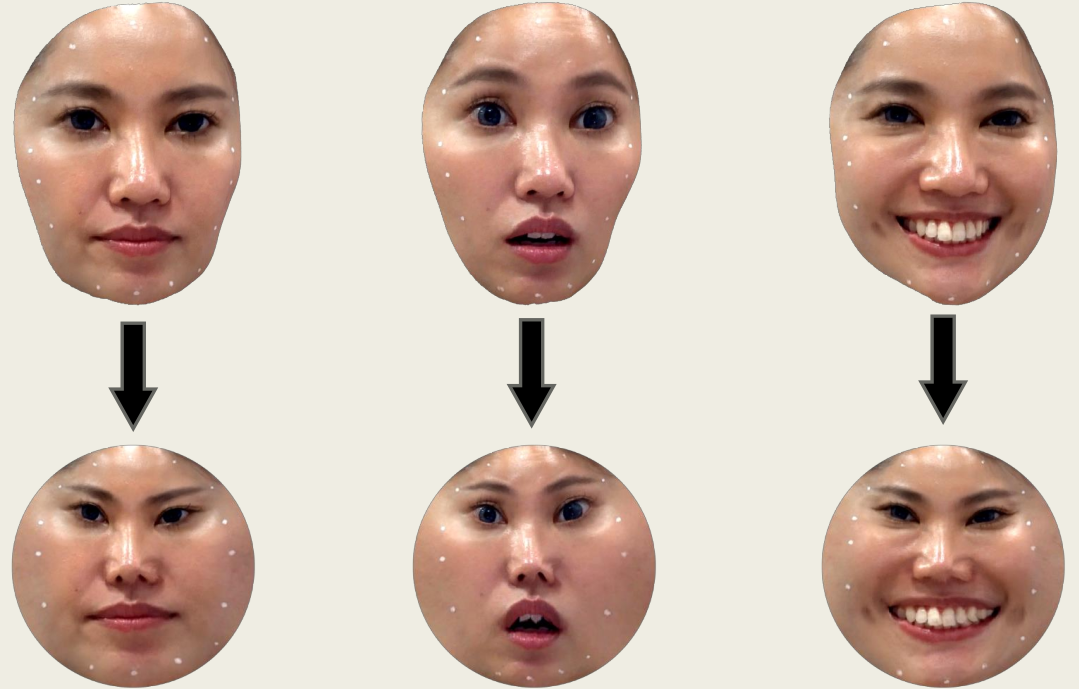
透过曲面的对应,建立曲面之间的平滑变化过程,称之为样条同伦。

最终利用共形变换和样条同伦实现三张三维照片之间的平滑动作变化——影像变形(Morphing)。

以及三维人脸的纹理贴图/虚拟化妆。

以及三维人脸的纹理重定向/虚拟化妆。

计算共形几何在医学图像领域有很多应用。例如虚拟肠镜技术。用 CT 扫描得到直肠曲面,再用共形映射将直肠曲面铺平在平面上。
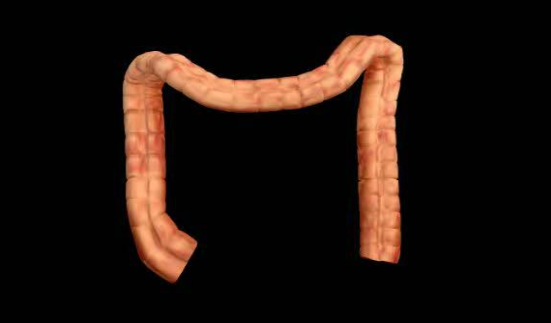
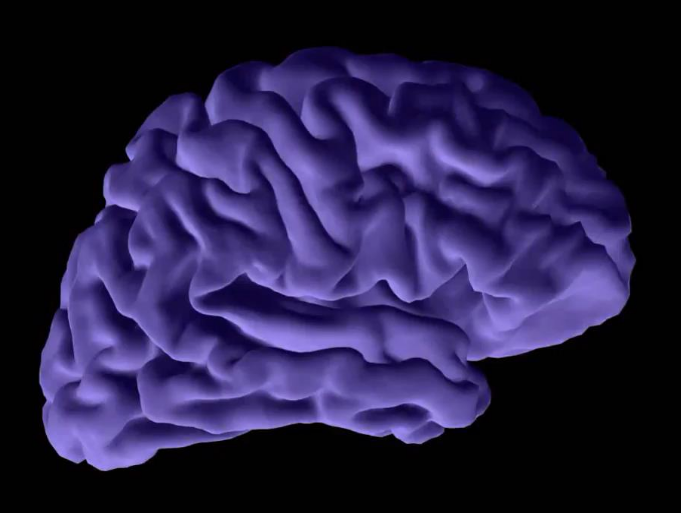
例如共形脑图技术。将核磁共振得到的大脑皮层曲面共形映射到单位球面,得到大脑皮层到球面的保面积参数化。
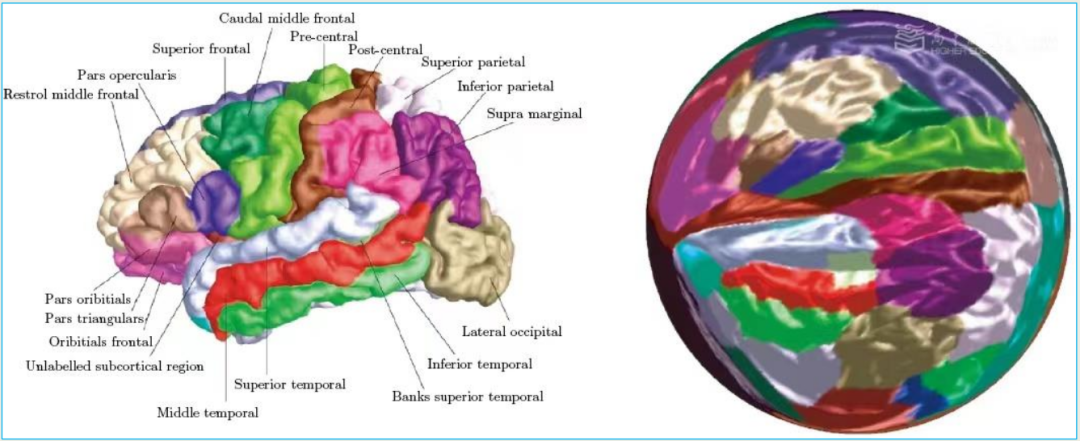
例如大脑曲面对应问题。利用拟共形映射参数化,准确地找出大脑曲面之间的点对点对应。大脑上可以找出对应的脑特征曲线,用以引导计算大脑曲面对应。
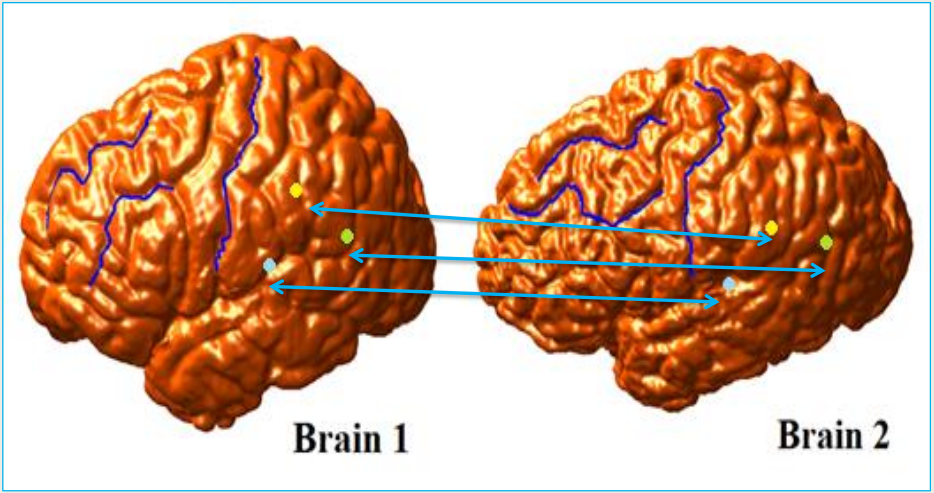
利用大脑曲面对应方法,可以有效地从一个大脑变换到另一个大脑,从而得出大脑曲面之间的点对点对应。可用于侦测器官中不正常的形状变化 (例如:追踪大脑萎缩的模式)。
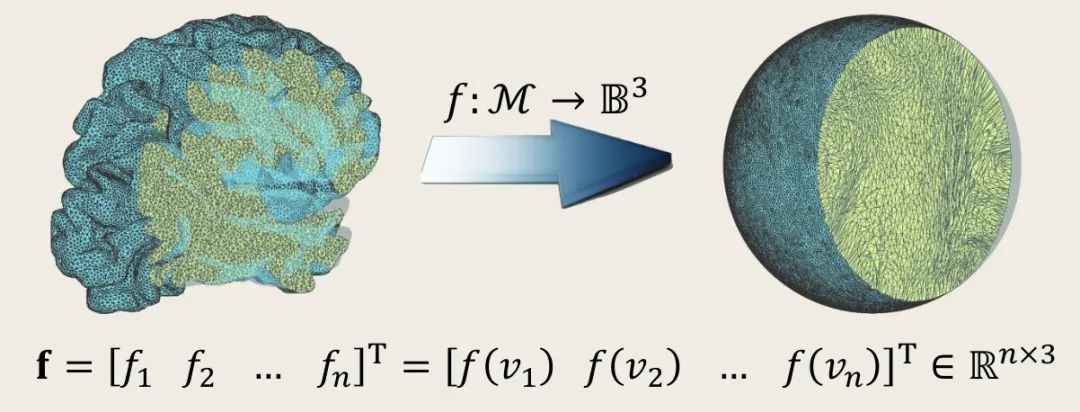
最优传输理论(optimal transportation)起源于法国数学家蒙日(Monge)于1781年提出的著名的最优传输问题。在欧氏空间中最优传输理论可描述为:区域上给定两个概率密度,存在保测度的自映射。在所有保测度的映射中,使得传输代价最小者被称为是最优传输映射。最优传输映射的传输代价被称为是两个概率密度之间的瓦瑟斯坦(Wasserstein)距离。
基于求解蒙日-安培方程的最优传输映射可以推广到任意维空间,这种方法(和林文伟、李铁香等合作)可以计算保体积和保质量的三维流形参数化:将不规则的三维体流形一一映射到单位球体上, 并保持体积畸变和质量畸变最小。
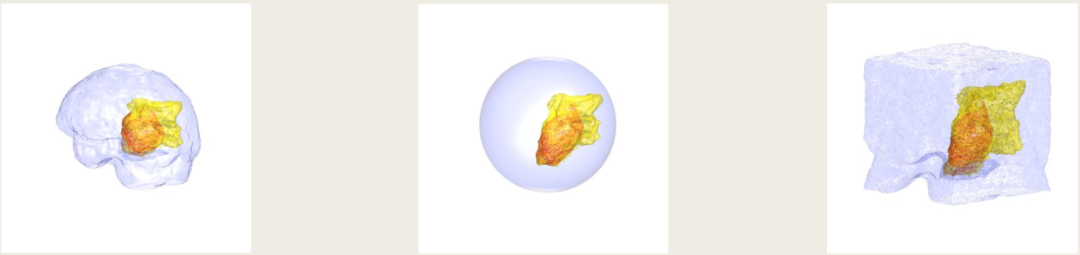
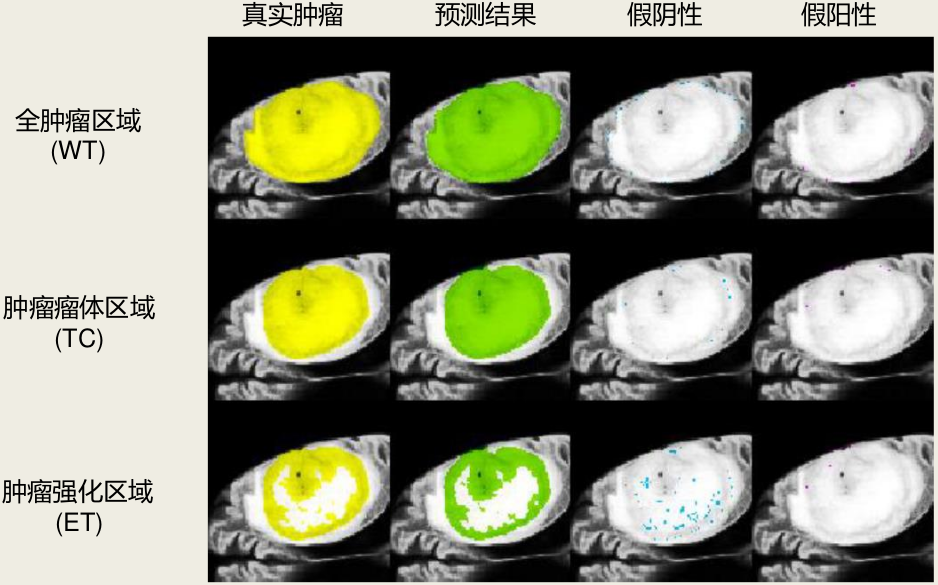
目前人工智能和数据科学的技术已被广泛应用于临床诊断、手术指导、风险预测等不同领域。例如基于最优传输的3D脑肿瘤分割与标注问题。
(1)基于最优传输理论可将3D脑图像以最小形变的方式映像到立方体中,可以用最少的储存量,保持脑图像的全局信息,作为机器学习的有效输入,达到脑图像的高精度的分割与注册。
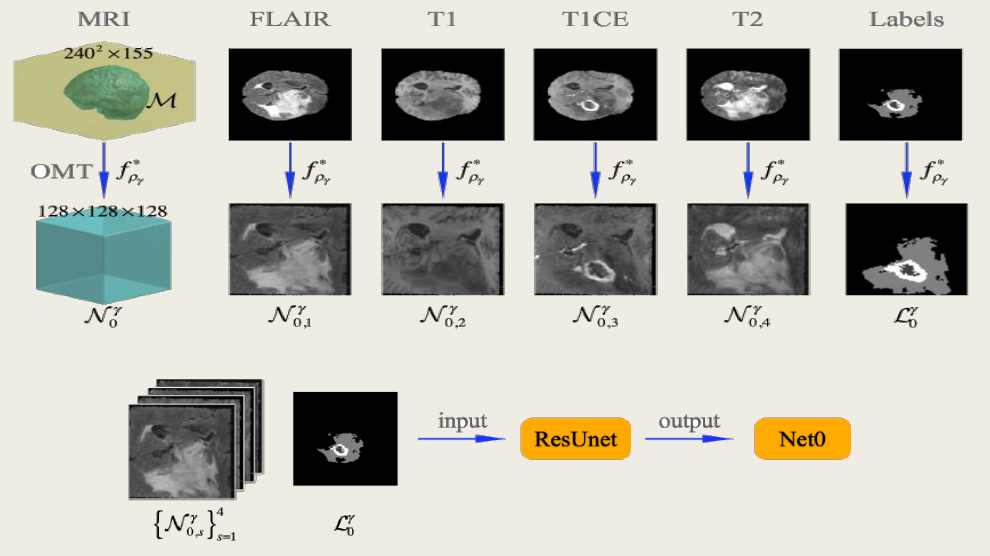
(2)每一个 MRI 脑影像包含四个模态,分别是 Flair, T1, T1CE和T2影像,分别代表不同扫描条件得到的脑核磁影像,每个坐标点都有对应的灰度值和肿瘤标签。将它们的灰度值作为密度,做步骤1中的最优传输映射。四个模态和标签数据形成的立方体共同成为深度学习的样本集。

3)基于最优传输的深度学习算法:利用3D U-net神经网络对样本集进行训练,最终将得到的 WT、TC、ET区域利用最优传输的逆映射反馈至原始的3D大脑影像。目前我们对WT、TC、ET的分割精度为93.71%,90.61%和87.47%。
脑肿瘤预测结果(局部放大)

目前人工智能由于计算器速度限制,只能采取多层状结构解决问题,无法有效地找出最优解。在可见得未来,如何提升量子计算机的硬件,发展更有效的数学算法,让量子人工智能与量子深度学习变成实用工具,这有赖于基础科学和数学的深度结合。
现代数学为人工智能奠定了理论基础,并且为人工智能突破瓶颈指明了发展方向;人工智能为数学提出了挑战,推动了数学的发展。
除了几何外,代数和数论对现代保密系统有极为重要的贡献,例如RSA保密系统的发现。
传统密码需要大量密钥,以致密钥的分配及管理极为困难,现代保密的常用做法是由李维斯特(Ron Rivest)、沙米尔(Adi Shamir)、阿德曼(Leonard Adleman)于1978年提出的(即RSA算法)。它的安全性是基于大整数分解。由于加密钥可以公开,因此称为公钥密码。
解密算法依赖于数论中的费马小定理,破解RSA密码的主要方法——大数分解是数论中一个重要课题。
现今最快的大数分解算法依次为:二次域筛法、数域筛法、椭圆曲线法。这些算法均建基于深刻的数学上。
在2002 年,三位印度数学家阿格拉瓦尔(Manindra Agrawal)、卡亚尔(Neeraj Kayal)和萨克塞纳(Nitin Saxena)发现如何用快速方法来决定一个大整数是素数的方法。这个方法有助于上述 RSA 中因子分解的问题。
清华大学王小云教授在密码破解上做出了重要的贡献。
近六十年来电脑的计算迅速与安全,一个重要原因是快速傅里叶变换(fast Fourier transform, FFT)的引入。它是快速计算序列的离散傅里叶变换(discrete Fourier transform,DFT)或其逆变换的方法。傅里叶分析将信号从原始域(通常是时间或空间)转换到频域的表示或其逆变换。FFT 通过把 DFT 矩阵分解为稀疏(大多为零)因子之积来快速计算此类变换。因此,它能够将计算DFT的复杂度从只用DFT定义计算需要的O(n2),降低到![]() ,其中 n为数据大小。
,其中 n为数据大小。
FFT 广泛的应用于工程、科学和数学领域。这里的基本思想通过库利(James William Cooley)和图基(John Wilder Tukey)在1965年才得到普及,但早在1805年就由高斯在《由一种新方法处理的插值理论》(Theoria interpolationis methodo nova tractata)中推导出来了。1994年美国数学家斯特朗(Gilbert Strang)把 FFT 描述为“我们一生中最重要的数值算法”,它还被 IEEE科学与工程计算期刊列入 20 世纪十大算法之一。
在现代工程依靠的数学中,控制理论占据着重要的地位。其中有滤波器(filtering)问题,它是透过有杂讯的观测值,预测无法被直接观测的内在状态。具体应用在导航和制导系统、雷达追踪和声纳测距,以及卫星和飞机的轨道计算中。
信号观测模型中最著名和通用的滤波器由卡尔曼(Rudolf Emil Kálmán)在六十年前提出。在处理讯号时,都要用到卡尔曼滤波(Kalman filter),但是它处理的是线性问题。
在实际情況下,我们需要考虑非线性的情形。我和我的弟弟丘成栋在二十年前找到了非线性滤波的计算方法,非线性滤波问题是通过信号观测模型的历史数据,从而获得事实数据的估计。
我们的方法(Yau-Yau滤波理论)可以通过求解柯尔莫哥洛夫(Kolmogorov)方程来估计状态向量。而柯尔莫哥洛夫方程是不包括随机变量的方程。

丘成栋(左),柯尔莫哥洛夫(右)
二十世纪科技的大改革,基础在于人类对于物质结构的深入了解。相对论和量子力学是这些学问的基础,数学家都对这些学问有深入的贡献!
庞加莱对狭义相对论,希尔伯特、外尔、冯诺依曼等人对于量子力学的贡献极为巨大,却没有受到应有的尊重。这些理论都极有深度,却是基于线性方程来发展的。爱因斯坦的广义相对论则由黎曼而来,却是基于非线性方程。在现象界里见到的,其实都是非线性现象。

从左至右:庞加莱、希尔伯特、冯诺依曼
自从七十年代高能物理学的标准模型建设成功,统一了物理学三个不同的场以后,物理学家的最大愿望是如何将引力放在标准模型中。
这个融合需要极有创意的观念的突破,我相信它对二十世纪期待的科技突破——量子计算,会有深度的影响。
如何构造量子几何学将会是一个重要的里程碑。最后也是真和美的结合!
我在上面枚举了数学在现代科技的应用,它们基于:
几何学家对于如何有效地将曲面美的特征表现出来的处理。
素数的分布,椭圆曲线上整数解的美丽理论,成为近代保密系统极为重要的工具。
波的有效描述,傅立叶变换产生的位置和动量对偶,对于现代科学,甚至计算科学,产生了基本上的变化!
只有美丽动人的基础数学提供出来的真理,可以放诸四海而皆准,流传万世而不竭!
万物之散聚兴灭,天地宇宙之结构,人事社会经济之脉络,莫不与基础数学有关。今日中国的复兴,不单单是解决所谓“卡脖子”的问题,也要建立千年王业的根基。泱泱大国,岂无文化深入的内涵,敦睦百国的风范?数学能够提供真和美,中华五千年要求的善,孔孟所说的仁和义,都可以在真和美中寻找,也就是说从数学学海中呼之而出。所以基本数学,是立国的基本,东西文化的桥梁。中华文化能够传承下去,千万年不衰,不可以不注重基础数学。
谢谢!
